Infinity comes in different sizes.

That statement startles most math majors when they first learn about sets. It’s counterintuitive on one level, as we are taught from an early age that there is only one infinity. But if I tell you that 2²²²²  and 2³⁰⁰⁰ are very large numbers, but the first is the larger of the two, then there is no controversy. We can have notions of “a very large number,” and “an even larger very large number” and everything is right as rain.

The smallest infinity is the one associated with the natural numbers:

0, 1, 2, 3, 4, 5, …

For simplicity, we label the set of natural numbers by the symbol N.  The set N is countable in the sense that its elements, the natural numbers, can be listed in succession. In a sense, N is the prototypical countably infinite sense, as saying a set is countable means that its elements can be matched up with the natural numbers.

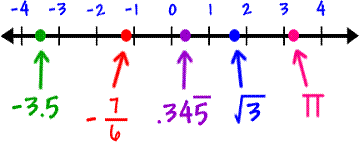
What about the infinity associated with a line, or continuum? Here we allow for numbers filling in the gaps between the natural numbers, like 1.5 or 27.3232782 or π.  We use the label R for the set of real numbers representing the continuum.

By an argument called diagonalization, we can show that the set of real numbers is not countable, or rather, it is uncountable. The sketch of the proof is to assume, wrongly, that R is countable, and list each real number with its decimal expansion. Then choose a new real number r that has a different decimal expansion with everything already in the list. We do this by making sure that for all i, the ith decimal of r is different from the ith decimal of the ith number in the list. The new real number r we created is not in the list, which is a contradiction.

Diagonalization shows us that the infinity associated with N is smaller than the infinity associated with R. What’s more, by taking the collection of all sets of real numbers, we find a set (called the power set of R) that has a larger infinity with R. By taking more and more power sets, we build up a never-ending sequence of infinities, each larger than the previous.

CH

Mathematicians like to order things. We’ve seen in the last paragraph that there is a never-ending sequence of increasingly larger infinities. The smallest of these is the infinity of N, and we know that the infinity on R is the larger of the two.

Is there anything in between them?

The continuum hypothesis (or CH) answers this question in the negative; that is, it states that the next largest infinity after the one for N is the infinity of R. While this might appear like an innocent-seeming statement, it’s been a central question in mathematics since it was first stated by Georg Cantor in 1878.

Axioms

Besides counting, mathematicians like to introduce axioms to study things in a systematic fashion. If you’ve studied linear algebra, you’ve seen this with the vector space axioms, or perhaps you’ve seen the axioms of a topological space or a matroid.

Set theory is a branch of mathematics where one develops axioms for sets and how they are put together. For some, this represents an attempt to give a foundation for all of mathematics. We call this kind of work metamathematics.

The most well-known set theory axioms are the ZFC axioms or the Zermelo-Fraenkel axioms with the Axiom of Choice. ZFC is widely accepted, and most working mathematicians don’t worry too deeply about these axioms or their consistency.

Logicians and set theorists, however, care a great deal about ZFC. Kurt Gödel showed in 1940 the relative consistency of ZFC along with CH. That is, he built a model for set theory where CH is true. This model, called L, asserts a very precise way of building subsets via first-order sentences, which ultimately allows the subsets to be better controlled. This extra control yields a proof of CH.

On the other hand, in 1963 Paul Cohen developed a new technique called forcing which builds models of set theory where ZFC holds but CH fails. Hence, CH is independent of the other axioms of set theory as it can be true or false depending on your model of ZFC.

But a mathematical statement can’t be true or false at the same time. Or can it?

CH has an answer

I would like to think that CH does have an answer, in the sense that other now solved major mathematical problems like the Poincaré conjecture or Fermat’s Last Theorem have definitive answers. I think the validity of CH is something we don’t have the mathematics in the present day to answer, regardless of the ground-breaking work of Gödel and Cohen.

The contemporary set theorist Hugh Woodin has set out a mathematical program to investigate CH by investigating what are called large cardinal axioms. This is a direction called inner model theory, where we build up the universe of sets from L into something more expansive where very large infinities can exist.

Woodin talks elegantly about CH in the following video.

As Woodin states in the video, there is no satellite we can build to measure CH. We can’t spend billions of dollars on a big particle collider and settle CH.

To me, CH represents a profound challenge to us as we grapple with mathematical truth. It’s a tantalizing mathematical problem staring at you each time you draw a line on a piece of paper.

Anthony Bonato