Ghost in the Machine
A clever way to foil an evil ghost possessing your computer is to ask it compute all the digits of π. Spock did just that in a scene from the classic Star Trek episode Wolf in the Fold.
But what exactly is π? It’s a number of course, but not like the counting numbers 1, 2, 3, … we learn in elementary school. The number π is arguably the most famous number in our culture, and for good reason: it is found in all over mathematics and the sciences.
The first three digits of π are 3.14, and that inspired Pi Day, which takes place on March 14 of each year (third month, fourteenth day, get it?). Some celebrate it exactly at 1:59 pm that day in honor of the next three digits: 3.14159… That date also happens to be Albert Einstein’s birthday. Go figure.
With Pi Day coming up next Monday, I am devoting the present blog to tour mathematical properties of π in layperson’s terms. Think of this as a condensed fact sheet if you are ever want to impress someone with your knowledge of π at a party.
Circles
π = C/D.
Note that this holds not just for a particular circle with a given diameter, but it also holds for any circle. So something is going on here that is fundamental. The above ratio is always the same number, and that number is nothing but π.
Here is how to practically illustrate π to anyone. Take a piece of string with length 1/2 (of any fixed distance: a half foot, meter, centimeter, etc.), and tie one to a pen or pencil. Press down one piece of the string or fix it with a pin, and draw a circle with the pen forming a circle whose diameter is D = 1. The length of the circle you just created is π.
Another illustration of how you can concretely think of π is in the following animation. The wheel of diameter one rolls out a length of exactly π.

Transcendence
As Mr. Spock says in the video clip, π is a transcendental number. To many people, it may be the only transcendental number they know. But what does this mean exactly?
Let’s back up a bit and discuss rational and irrational numbers. A rational number is a fraction of integers. For example, 22/7 = 3.1428… is rational, and this fraction has been used historically as an approximation of π.
Not every number is rational, however. For example, √2 is irrational, meaning it is not of the form a/b for some integers a and b. But √2 is the solution of a simple polynomial equation:
x2 = 2.
A transcendental number is not the solution to any polynomial equation whose coefficients are rational:
![]()
That is saying a great deal, as such equations can be any degree and with any choice of coefficients.
Johann Heinrich Lambert proved that π is irrational much earlier in 1761. Ferdinand von Lindemann proved in 1882 that π is transcendental. Lindemann’s proof was a breakthrough, as great mathematicians like Euler tried to do it but failed.

An interesting fact is that there infinitely many transcendental numbers (in fact, uncountably many; skip the next sentence if you don’t know what this means). The existence of transcendental numbers follows by a simple argument: there are only countably many polynomials with rational coefficients, but there are uncountably many real numbers.
Despite their abundance on the real number line, proving any given number is transcendental is hard or even unsettled. For example, we don’t know if ππ is transcendental. Another important transcendental number is e = 2.718…, which comes up for example, in the study of compound interest. While we know that eπ is transcendental, we don’t know if π + e or π – e are transcendental!
Problems like these I find humbling. They remind us despite our incredible progress over the last few centuries as a species, we have really only begun to understand the field of mathematics.
History of π
One of the first recorded instances of π comes from the Rhind Papyrus (which dates around 1650 BC), which shows that the ancient Egyptians calculated the area of a circle using an approximate value of 256/81 = 3.1605. A Babylonian tablet (around 1900–1680 BC) showed a value of 3.125.

Archimedes found a more precise value of π. His idea was simple but very elegant. Inscribe regular polygons inside and outside a circle to approximate its area. The more sides you used, the better the approximation. The method nicely illustrates the notion of a limit that we teach in Calculus. As the area of polygons is easily derived; for example, split the polygon into smaller triangular wedges and sum up their area. Archimedes’s method gives both upper and lower bounds for the area. Using this approach, he found that 3.1408 < π < 3.1429, which is accurate to three digits.
Ancient Indians, Persians, and Chinese scholars also reference π in their works. Interestingly, it wasn’t until 1706 when the mathematician William Jones (a friend of Newton’s) adopted the symbol π.

Computing π
I memorized the first fifteen digits of π as a teenager, but that is nothing compared to Rajveer Meena. He holds the world record of memorizing 70,000 digits. It took him ten hours to recite these in March 2015 while wearing a blindfold. I suppose we all need our hobbies.
 π has a never-ending sequence of digits in its decimal expansion. As it is irrational, the decimals don’t repeat in any simple pattern. There is a conjecture that π is a normal number, which means roughly that its digits behave as if they were chosen randomly. For example, any single digit in a normal number occurs one-tenth of the time, two digits appear 1/100 time, three 1/1000 times, etc. No one can prove this yet about π, although evidence suggests it may be true. In 1995, Yasumasa Kanada computed the first six billion digits of π and found that each of the ten digits: 0, 1, 2, …, 9 occurred 600 million times. You would expect this if π were a normal number.
π has a never-ending sequence of digits in its decimal expansion. As it is irrational, the decimals don’t repeat in any simple pattern. There is a conjecture that π is a normal number, which means roughly that its digits behave as if they were chosen randomly. For example, any single digit in a normal number occurs one-tenth of the time, two digits appear 1/100 time, three 1/1000 times, etc. No one can prove this yet about π, although evidence suggests it may be true. In 1995, Yasumasa Kanada computed the first six billion digits of π and found that each of the ten digits: 0, 1, 2, …, 9 occurred 600 million times. You would expect this if π were a normal number.
There were many formulas used to compute π through history. Usually, these formulas involve adding, subtracting, multiplying, or dividing an infinite number of terms or a series. A simple one for finding digits is the following infinite alternating series, discovered by Leibniz in the 17th century:
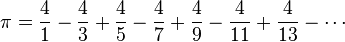
This series, while elementary looking, takes a very long time to converge: after summing 500,000 terms in the alternating sum, it only gives five correct decimal places!
A faster approach is to use the expression of John Machin from 1706:

This too leads to a series expansion for π using the Taylor expansion for arctan, and Machin used it to compute the first 100 digits.
The Machin formula was used by many to find new decimals of π. Now more sophisticated formulas and methods are known. There are dozens of infinite series and infinite products giving π. The most famous one is due to the Chudnovsky brothers, and is based on the convergent generalized hypergeometric series:

The Chudnovsky formula converges much faster and reaches 51 digits of precision with just four iterations. There is even an on-line Java program that implements the Machin and Chudnovsky formulas.

The world record for the largest known digit of π is held by Nicholas Sze at Yahoo, who computed the 2 quadrillionth (= 2,000,000,000,000,000) digit in 2010. The computation took twenty-three days using 1,000 computers using the MapReduce approach. If you are curious, the 2 quadrillionth digit of π is 0. The world record for computation of the largest number of each of the digits from 3 onwards is held by Peter Treub, who computed the first 22.4 trillion digits of π in November 2016. He used the y-cruncher program, which has broken previous world records.
Applications of π
The number π comes up in virtually every branch of mathematics. Many of us see it first in basic geometry and trigonometry, but it plays a central role in advanced mathematical topics in number theory, combinatorics, probability, and complex analysis.
For instance, people usually refer to Euler’s identity as one of the most beautiful and famous in all of Mathematics:
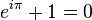
Here, i is the complex constant satisfying i2 = −1. This one equation ties together the transcendental numbers π and e, along with i, and the multiplicative and additive identity elements 1 and 0, respectively. Good stuff!
We find π in unexpected places and unexpected regions of mathematical research. A partition of a positive integer n is one way of writing n as a sum of positive integers. For example, 5 equals: 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1 and also just 5. This is expressed simply as P(5) = 7, corresponding to the seven ways to write 5 as a partition. In 1918, Ramanujan and Hardy gave a beautiful expression for P(n) for any integer n:

The formula is asymptotic: while not giving the precise value, the formula gets more and more accurate as n tends to infinity. The asymptotic partition formula of Ramanujan and Hardy is a centerpiece of the fabulous upcoming movie The Man Who Knew Infinity (see my review; I was lucky enough to see the world premiere at the Toronto International Film Festival in September 2015).

We also find π in many formulas from the sciences and engineering. We find that π comes up in the study of gravity, electromagnetism, fluid dynamics, and signal processing, to name a few disciplines.
Einstein’s field equation, which describes gravity as arising from the curvature of space-time, is:
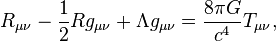
which has been used to predict the existence of black holes and gravitational waves. Gravitational waves were discovered in February 2016 about 100 years after Einstein predicted them, sending shock waves through the scientific community.
/cdn0.vox-cdn.com/uploads/chorus_asset/file/6030221/gravitywaves.gif)
Pi Day
The number π is so cool it gets its own day. Not many other numbers can boast such a reputation. As you might expect from the name, many people unleash their inner culinary geek to celebrate Pi Day by making all kinds of pies.

Have a happy Pi Day!

Anthony Bonato

[…] via Everything you wanted to know about pi but were afraid to ask […]
LikeLiked by 1 person