ICYMI. From the archives. Enjoy! -AB
***
Mathematics speak
Mathematics is one of the several ways we communicate, allowing us to grapple with the complex patterns abundant in the universe. If I state that “The number of non-isomorphic groups of order 16 is 14,” then that means something to most mathematicians. It may mean more to some; in particular, those who study groups, or group theorists.
Group theorists have their own peculiar language. They make statements such as “If G* is a simple K-group, then the core of the centralizer of an involution of G* is cyclic,” which only makes sense if you know the subject.

Learning advanced mathematics like modern group theory takes thousands of hours of study. I suppose in that way it is like learning a foreign language. Some of us are more fluent in mathematics, while others speak broken mathematics largely consisting of arithmetic, trigonometry, or Calculus.
Not so fast
A fascinating recent study by French neurobiologists Marie Amalric and Stanislas Dehaene reached an interesting conclusion: mathematical thinking, whether basic or advanced, resides in a nonlinguistic part of the brain. Our brains process language and mathematics differently.

Here is the full reference to the paper:
Marie Amalric and Stanislas Dehaene, Origins of the brain networks for advanced mathematics in expert mathematicians, Proceedings of the National Academy of Sciences,
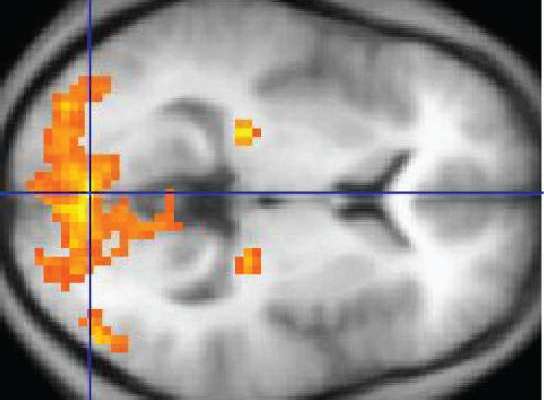
For the curious mathematicians out there, here is your brain on math (figure taken from the paper), shown in group A on the left.

What they did
Using functional magnetic resonance imaging, Amalric and Dehaene studied the brains of 15 mathematicians vs 15 non-mathematicians (who acted as controls) while they each studied mathematical and non-mathematical statements. Subjects had to make judgments on whether the statements were true, false, or meaningless. The mathematical statements contained higher mathematical subject matter: analysis, algebra, topology and geometry. The linguistic statements were non-mathematical but of parallel complexity, taken from topics related to nature or history.
The mathematicians, as you would expect, were better able to detect the mathematical meaning in statements, while the control group fared much worse. The control group, however, performed well with the non-mathematical statements.

The brains of the mathematicians were active in the bilateral intraparietal, inferior
temporal, and dorsal prefrontal sites. These are the areas that correspond to the processing of basic arithmetic; this, perhaps more than anything other discovery in the paper, comes as a big surprise to me. The parts of your brain used for adding or multiplying numbers are the same parts used for advanced mathematics in topics like algebra and topology. Non-mathematical statements did not activate these areas.
What the study means
The authors conclude that language and mathematics are processed in different parts and in different mechanisms of the brain of mathematicians. The regions of the brain involved in mathematical reasoning are known to also correspond to problem-solving and are not viewed exclusively as processing mathematical thinking.
If the brain areas related to basic and advanced mathematics are the same, then these findings actually corroborate earlier educational studies that show that early proficiency in mathematics can predict later success in mathematics.
To mathematicians, the study implies that the work we do is not based on language skills. The way we think about mathematics is fundamentally distinct from language.
The authors cite a prescient quote from Einstein, who said: “Words and language, whether written or spoken, do not seem to play any part in my thought processes.” Interestingly, Einstein’s brain has been studied intensively after his death.
That is not to say that we don’t use language to describe mathematics; far from it; the tens of thousands of mathematical research papers and books published each year do just that. I chat all the time with mathematician collaborators at chalkboards, over coffee, and over Skype. We talk about mathematics interspersed with English to examine the truth of our proposed theorems.
My experience with mathematics and language
During my doctoral degree, I was required to translate a mathematics paper written in French into English. Although I passed the exam with ease (despite my monolingualism) my advisor chose a dense paper with a plethora of complex compound sentences.

From a certain point of view, the study of Amalric and Dehaene gels well with my experience. I am adept at mathematics and enjoy studying and teaching the subject. Speaking multiple languages, however, is not my forte.
I don’t think mathematics and language skills are mutually exclusive, however, and nothing in the study suggests that conclusion. For example, I enjoy creative writing as hobby distinct from my mathematical research. Many of my colleagues, however, are both brilliant mathematicians and speak multiple languages (one I know speaks six).
Mathematics is its own unique language
Mathematics is about patterns: recognizing and classifying them. These patterns are often complex, and we have limited ways to describe them. These patterns come from nature, from physical, biological, or social systems, but also they are patterns which stand by themselves, like prime numbers or finite simple groups.
I put forward a complementary thesis, one that has no formal basis in neuroscience, but comes from my own experience as a working mathematician:
My view is that mathematics is its own special type of language.
Mathematics is unique among languages, however, in that it is fundamentally based on reasoning and logical inference. In contrast, while the grammar of a language such as English has logical aspects, it is highly arbitrary. Nouns and verbs must be memorized for each language, and assigning gender to inanimate objects like chairs or bikes always seemed odd to me.
As students of mathematics know, a great deal of linguistic recognition is needed to learn the subject. If I state Tutte’s conjecture as “Every bridgeless graph has a nowhere-zero 5-flow,” then the sentence is meaningless unless you understand the context of the phrases “bridgeless graph” and “nowhere-zero 5-flow.” However, understanding the real meaning behind Tutte’s conjecture requires mathematical, not just linguistic knowledge. In fact, no one really understands it, as it is an open problem!

As my mentor, the late lattice theorist Gunter Bruns would emphatically say when teaching his undergraduate algebra courses: “I love abstraction.” I view my own skills with basic arithmetic as fair at best. The study makes me wonder if I am selling myself short on my elementary school level arithmetic abilities. I have a near eidetic memory with numbers, and I can calculate a tip in a restaurant usually faster than anyone else can. I found the rote learning of multiplication tables boring. Arithmetic just seemed so arbitrary. My first real excitement with mathematics came when I learned about infinite sets and that the cardinality of the real number system is uncountable.
That abstract knowledge, not adding numbers, blew my mind.
Other questions
The paper of Amalric and Dehaene provides some hard scientific insights into how we think about mathematics. As all good science does, it raises more questions than it answers.
Mathematics is communicated via your everyday language. How do the mathematical and linguistic parts of your brain interact? The two parts must work synergistically. Understanding complex systems like the neural networks in our brains is a deep and not well-understood area.


I am also curious about the relationship between art and mathematics. Do artists use their brains in any way like mathematicians? A 2014 study by neurobiologist Seth Zeki (which included an eminent mathematician Michael Atiyah in the list of authors) claims that recognizing mathematical beauty correlates with finding beauty from other sources such as paintings or music.
What can be said about the brains lawyers? Do their brains function like mathematicians? They can be analytic as the best of us.
Lawyers, after all, are the only other profession I know that also call things trivial.
Anthony Bonato
[…] Group theorists have their own peculiar language. They make statements such as “If G* is a simple K-group, then the core of the centralizer of an involution of G* is cyclic,” which only makes sense if you know the subject. … (The Intrepid Mathematician) […]
LikeLike